Image Recognition With Deep Learning: Neural Networks

In this task, we will train a neural network model to classify images it has not seen before. This is the "Hello World" of deep learning.

The model will be trained to recognize patterns in images through trial and error as it learns on 60,000 images in 10 different classes. We will use the CIFAR10 dataset, which has the following image categories:

Loading the dataset

To start with, the dataset will be divided into 4 segments:

1. x_train: A collection of 50,000 images used to train the neural network.
2. y_train: The corresponding labels for these images (e.g., bird, cat, deer, etc.).
3. x_test: A set of 10,000 images used to validate the model's performance after training.
4. y_test: The correct labels corresponding to the x_test dataset.

We will use Keras API, which offers many useful built-in functions specifically designed for image recognition and other computer vision tasks. Another useful feature of Kera is its built-in modules that provide helper methods for handling several datasets, including CIFAR-10. We start by loading the database into memory:

(x_train, y_train), (x_test, y_test) = tf.keras.datasets.cifar10.load_data()

Let's visualize a subset of data to view a few images, their corresponding labels, and their class index:

Preparing the dataset

As seen in the images above, the labels are integers between 0 and 9, representing the 10 classes. Ensuring that the model consistently selects the correct category during predictions is crucial. Therefore, we should deal with the issue of proximity-based errors with numerical labels. For instance, if we train our model using numerical labels from 0 to 9 and present it with a test image of a deer labeled as 4, the model may mistakenly predict it as 3, which corresponds to a cat. The model's inability to distinguish the subtle difference between 3 and 4 leads to wildly inaccurate predictions. However, by employing categorical encoding, we can overcome this issue and significantly improve the model's accuracy.

num_classes = 10
y_train = keras.utils.to_categorical(y_train, num_classes)
y_test = keras.utils.to_categorical(y_test, num_classes)

Categorical encoding modifies the data so that each value is a collection of all possible categories, with the correct category value set to 1 and the others set to 0. Since our categorical variable takes a relatively small number of values (<15), we will use one hot encoding, which creates binary columns, indicating each value from the data with the correct value set to 1.

Imagine we are encoding the first image in x_test, which is a picture of a frog with a label value of 6. One-hot encoding will create a separate column for each label value, setting the correct label to 1 and the rest to 0.

Next, we also need to flatten or vectorize our images. For example, the shape of our x_train dataset is (50000, 32, 32, 3), which is 50,000 color images of size 32x32. We will convert each image to a 3072-dimensional (32x32x3) vector, which simplifies the image input to the model.

x_train = np.reshape(x_train, (50000,3072))
x_test = np.reshape(x_test, (10000,3072))

Finally, we also need to normalize our new 3072-dimensional data values to a standard range of 0 to 1. This normalization enables the model to train faster and make better predictions.

However, to do this, we need to know the maximum and minimum values for each vector, which are as follows in our dataset:

Minimum value of x_train: 0.0, Maximum value of x_train: 255.0

By dividing the pixel values of images by the maximum value, we normalize these values to a range of 0 to 1.

x_train = x_train / 255
x_test = x_test / 255

Training the model

Now that the data is ready, it is time to train the model. But first, we need to create the model with the prepared data for training. The following is a basic model composed of an input layer, several hidden neuron layers, and an output layer to depict the network's prediction for a given image.

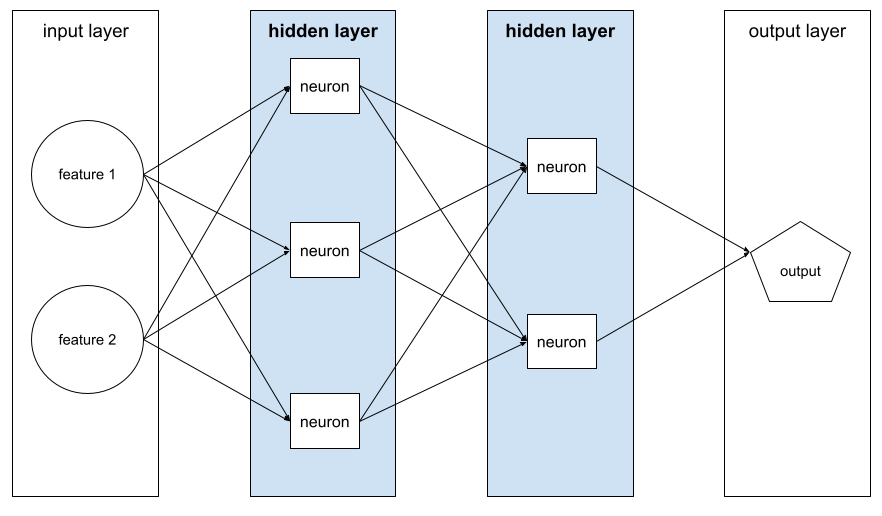
Notice that each neuron is interconnected with all other subsequent neurons in the following layers. The neurons in the first hidden layer compute the weighted sum of input values from the input layer (features 1, 2, etc.). As for neurons in any subsequent hidden layer, they receive input from neurons in the preceding hidden layers. In essence, a neuron in a neural network emulates the behavior of neurons in human brains and other parts of the nervous system.

To start building the model, we will use Keras's Sequential model class, which allows us to instantiate a model and add multiple layers. With the Sequential model, the data flows through the model in a sequential manner, layer by layer.

from tensorflow.keras.models import Sequential
model = Sequential()

Next, we will add the input layer, which is densely connected. This means that each neuron and its weights will impact every neuron in the subsequent layer.

from tensorflow.keras.layers import Dense
from tensorflow.keras import activations

model.add(Dense(units = 512, activation = 'relu', input_shape=(3072,)))
model.add(Dense(units = 512, activation = 'relu'))
model.add(Dense(units = num_classes, activation='softmax'))

The output of these dense layers is an m-dimensional vector. We utilize the rectified linear activation function (ReLu) in both the input and hidden layers. This function directly outputs the input of the respective layer if it is positive; otherwise, it outputs zero. This choice enhances performance and facilitates easier model training.

Furthermore, the "units" argument specifies the number of neurons in each layer. Each hidden layer will have 512 neurons, while the output layer will have a total of 10 neurons, corresponding to the 10 different classes. Below is a summary of the model:

Next, before training the network, we compile the model. To achieve this, we need to specify a loss function and include a metric for measuring the neural network's performance. The loss function quantifies how closely the model's predictions align with the actual labels. Since we have 10 categorical labels, we will calculate the loss using categorical cross-entropy. Lower loss values indicate better predictions, while higher loss values indicate less accurate predictions. Our goal is to minimize the loss returned by the loss function.

model.compile(loss='categorical_crossentropy', metrics=['accuracy'])

Finally, we are ready to train the model using the training data and validate it with the validation data. This process of training the model is often referred to as "fitting a model to data," and as such, we will use the fit method to accomplish this task.

history = model.fit(x_train, y_train, epochs=20, verbose=1, validation_data=(x_test, y_test))

Output:
Epoch 1/20
1563/1563 [==============================] - 47s 29ms/step - loss: 1.9163 - accuracy: 0.3122 - val_loss: 1.8826 - val_accuracy: 0.3157
Epoch 2/20
1563/1563 [==============================] - 46s 30ms/step - loss: 1.7080 - accuracy: 0.3874 - val_loss: 1.6453 - val_accuracy: 0.4118
-----
Epoch 19/20
1563/1563 [==============================] - 45s 29ms/step - loss: 1.5195 - accuracy: 0.4710 - val_loss: 1.6453 - val_accuracy: 0.4455
Epoch 20/20
1563/1563 [==============================] - 45s 29ms/step - loss: 1.5195 - accuracy: 0.4705 - val_loss: 1.6673 - val_accuracy: 0.4372

Notice the accuracy and val_accuracy scores. accuracy show how well the model did on the training data, while val_accuracy shows how well the model did on the validation data. Here's the accuracy and loss functions as shown in the following graphs:

Take note of the accuracy and val_accuracy scores. The accuracy represents how well the model performed on the training data, whereas val_accuracy indicates its performance on the validation data. Below are the accuracy and loss functions:

The model's performance on the training data needs improvement. To address this, our next step will involve using convolutional neural networks (CNNs), to significantly improve the model's validation and accuracy and achieve better predictions.

Source Code on Github